题目内容
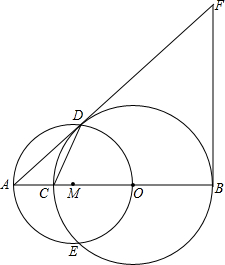如图，C为线段AB上一点，以BC为直径作⊙O，再以AO为直径作⊙M交⊙O于D、B作AB的垂线交AD的延长线于F，连接CD．若AC=2，且AC与AD的长是关于x的方程x2-2(1+| 5 |
①求证：AD是⊙O的切线；
②求线段DF的长．
分析：（1）连接OD，证OD⊥AD即可；已知AO是⊙M的直径，那么根据圆周角定理即可判定OD⊥AD，由此得证．
（2）由根与系数的关系可求得AD的长，进而可根据切割线定理求得AB的值；设出DF、BF的长，然后在Rt△ABF中，由勾股定理求出DF的长．
（2）由根与系数的关系可求得AD的长，进而可根据切割线定理求得AB的值；设出DF、BF的长，然后在Rt△ABF中，由勾股定理求出DF的长．
解答：
（1）证明：连接OD；
∵OA是⊙M的直径，
∴∠ADO=90°；
即OD⊥AD，而OD是⊙O的半径，
故AD是⊙O的切线．
（2）解：由题意知：AC+AD=2(1+
)；
已知AC=2，则AD=2
；
由切割线定理知：AD2=AC•AB，即AB=AD2÷AC=10；
由于FD、FB都是⊙O的切线，故FD=FB；
设FD=FB=x，则AF=2
+x；
由勾股定理得：AB2+BF2=AF2，即：
102+x2=（2
+x）2，解得x=4
；
即线段DF的长为4
．
（1）证明：连接OD；∵OA是⊙M的直径，
∴∠ADO=90°；
即OD⊥AD，而OD是⊙O的半径，
故AD是⊙O的切线．
（2）解：由题意知：AC+AD=2(1+
| 5 |
已知AC=2，则AD=2
| 5 |
由切割线定理知：AD2=AC•AB，即AB=AD2÷AC=10；
由于FD、FB都是⊙O的切线，故FD=FB；
设FD=FB=x，则AF=2
| 5 |
由勾股定理得：AB2+BF2=AF2，即：
102+x2=（2
| 5 |
| 5 |
即线段DF的长为4
| 5 |
点评：本题主要考查了切线的判定、切割线定理、切线长定理、勾股定理以及韦达定理等知识的综合应用，难度适中．
练习册系列答案
考前必练系列答案
相关题目
如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，若AC=3，BC=2，则△MCD与△BND的面积比为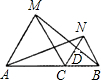
如图，C为线段AB上的一点，△ACM、△CBN都是等边三角形，BM与CN交于D点．若AC=3，BC=2，则CD=
7、如图，P为线段AB上一点，AD与BC交干E，∠CPD=∠A=∠B，BC交PD于E，AD交PC于G，则图中