题目内容
9. 如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=$\frac{4}{5}$.
如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=$\frac{4}{5}$.
分析 先根据圆周角定理求出∠ACB=90°,∠ADC=∠ABC,再由勾股定理求出BC的长,据此可得出结论.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,∠ADC=∠ABC.
∵AB=15,AC=9,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12,
∴cos∠ADC=cos∠ABC=$\frac{BC}{AB}$=$\frac{12}{15}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查的是圆周角定理,熟知半圆(或直径)所对的圆周角是直角是解答此题的关键.

练习册系列答案
相关题目
14.2016年9月15日,我国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.大约经过10分钟后,成功进入远地点350000米的初始轨道.将数据350000用科学记数法可表示为( )
| A. | 35×104 | B. | 350×103 | C. | 3.5×105 | D. | 0.35×106 |
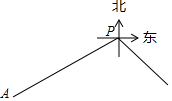
 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,∠ABO=30°,OB=3OC.
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,∠ABO=30°,OB=3OC.
 如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)