题目内容
13.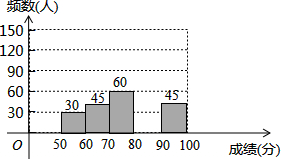 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
(1)表中m=120,n=0.2;
(2)补全频数分布直方图;
(3)在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学参加区级的比赛,用树状图或列表法求选出的两名同学恰好是一男一女的概率.
分析 (1)首先用1组的人数除以频率,求出全体参赛的选手人数有多少;然后用全体参赛的选手人数乘4组的频率,求出m的值是多少;最后用3组的人数除以全体参赛的人数,求出n的值是多少.
(2)根据80≤x<90的学生人数,补全频数分布直方图即可.
(3)在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),用树状图求出选出的两名同学恰好是一男一女的概率是多少即可.
解答 解:(1)由表格可得,
全体参赛的选手人数有:30÷0.1=300,
则m=300×0.4=120,n=60÷300=0.2.
(2)补全的频数分布直方图如右图所示, .
.
(3)如图,所有结果如下:
∵共有20种等可能的结果,两名主持人恰为一男一女的有12种情况,
∴则P(恰好选到一男一女)=$\frac{12}{20}$=$\frac{3}{5}$.
故答案为:120,0.2.
点评 此题主要考查了列表法与树状图法,以及频数分布表、频数分布直方图的应用,要熟练掌握.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
3. 如图物体的主视图是( )
如图物体的主视图是( )
 如图物体的主视图是( )
如图物体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
8. 如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
 如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
如图,AB∥CD,直线L交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )| A. | 105° | B. | 115° | C. | 125° | D. | 75° |
3.下列运算正确的是( )
| A. | m2•n2=(mn)4 | B. | 5x2y-4x2y=1 | C. | m-2=$\frac{1}{{m}^{2}}$(m≠0) | D. | (m-n)2=m2-n2 |
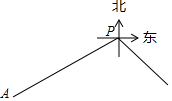 如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236) 如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017).
如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017). 如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )
如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )