题目内容
2.直角梯形的一腰长为10cm,其与底边所成的角为45°,那么另一端长为10$\sqrt{2}$cm.分析 如图作DE⊥BC于E点,根据∠DCE=45°,AB=DE=10可以求得DC的长.
解答 解:作DE⊥BC于E点,
∵梯形ABCD是直角梯形,
∴四边形ABED是矩形,
∴DE=AB=10cm,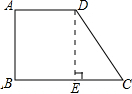
∵∠DCE=45°,DE=10cm,
∴DE=EC=10cm,
∴DC=$\sqrt{D{E}^{2}+E{C}^{2}}$=10$\sqrt{2}$cm.
故答案为10$\sqrt{2}$cm.
点评 此题考查了直角梯形中常用的计算问题以及勾股定理的运用.所作辅助线是直角梯形中常作辅助线,把直角梯形转化为矩形和直角三角形后求解.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.在数轴上到原点的距离等于5的点表示的数是( )
| A. | 5 | B. | 2 | C. | 5或-2 | D. | 5或-5 |
7.下列计算正确的是( )
| A. | (-1)-3=1 | B. | (-4)0=1 | C. | (-2)2×(-2)-3=26 | D. | 2a-4=$\frac{1}{{2a}^{4}}$ |
14.在2,3,0,1中,绝对值最小的数是( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
11. 张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
 张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )
张萌将直尺ABCD(AD∥BC)和三角板EFG按如图所示的方式摆放,点F在BC上,若∠BFE=20°,∠EFG=90°,则∠DMF的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
12. 如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
 如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵高5米,两树相距12米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A. | 8米 | B. | 10米 | C. | 13米 | D. | 14米 |