题目内容
12．
如图，有两棵树，一棵高10米，另一棵高5米，两树相距12米．一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行（ ）| A． | 8米 | B． | 10米 | C． | 13米 | D． | 14米 |
分析 根据“两点之间线段最短”可知：小鸟沿着两棵树的顶端进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．
解答 解：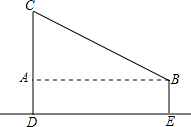
建立数学模型，两棵树的高度差AC=10-5=5m，间距AB=DE=12m，
根据勾股定理可得：小鸟至少飞行的距离BC=$\sqrt{1{2}^{2}+{5}^{2}}$=13m．
故选C．
点评 本题主要考查了勾股定理的应用，解题的关键是将现实问题建立数学模型，运用数学知识进行求解，难度一般．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
3．下列各数中，没有平方根的是（ ）
| A． | -32 | B． | |-3| | C． | （-3）2 | D． | -（-3） |
如图，木条a与木条c垂直，将木条a绕点O旋转后与木条b平行，则旋转角的最小值为22°．
如图，在平面直角坐标系中，A（-3，0），B（0，-4），C（4$\sqrt{3}$，0），D（0，4），点P、Q分别是线段AD、BC上的动点，AQ与BP交于点E，与y轴交于点F，∠BAD=180°-∠BEQ，设AP的长为x．
17．一个三位数，3个数位上的数字和是15，百位上的数字比十位上的数字小1，个位上的数字比十位上的数字大1，则这个三位数是（ ）
| A． | 345 | B． | 357 | C． | 456 | D． | 567 |
4．在平面直角坐标系中，点P（1，2）到原点的距离是（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
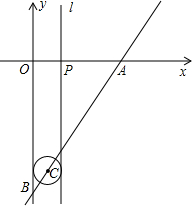如图，平面直角坐标系的单位是厘米，直线AB的解析式为y=$\sqrt{3}$x-6$\sqrt{3}$分别与x轴、y轴相交于A、B两点．点C沿射线BA以3厘米/秒的速度运动，以点C为圆心作半径为1厘米的⊙C．点P以2厘米/秒的速度在线段OA上来回运动，运动时间为t（t＞0），过点P作直线l垂直于x轴．