题目内容
11.若a<-2,$\frac{1}{a+2}$$\sqrt{\frac{(4-{a}^{2})(a+2)}{4}}$的化简结果是$-\frac{\sqrt{2-a}}{2}$.分析 首先将4-a2分解为(2+a)(2-a),然后依据$\sqrt{{a}^{2}}=|a|$进行化简即可.
解答 解:原式=$\frac{1}{a+2}\sqrt{\frac{(2-a)(a+2)^{2}}{4}}$
=$\frac{1}{a+2}•\frac{|a+2|\sqrt{2-a}}{2}$
∵a<-2,
∴a+2<0
∴原式=$-\frac{\sqrt{2-a}}{2}$.
故答案为:$-\frac{\sqrt{2-a}}{2}$.
点评 本题主要考查的是二次根式的性质与化简,将4-a2分解为(2+a)(2-a),然后依据$\sqrt{{a}^{2}}=|a|$进行化简是解题的关键.

练习册系列答案
相关题目
1.若a满足不等式组$\left\{\begin{array}{l}{2a-1≤1}\\{\frac{1-a}{2}>2}\end{array}\right.$,则关于x的方程(a-2)x2-(2a-1)x+a+$\frac{1}{2}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 以上三种情况都有可能 |
 如图,x是△ABC一边的长,则x的取值范围是1<x<5.
如图,x是△ABC一边的长,则x的取值范围是1<x<5.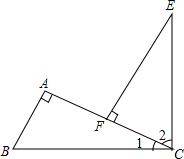 如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗?
如图,∠A=90°,BC⊥EC,EF⊥AC,BC=CE,你能根据以上的条件,说明△ABC≌△FCE吗? 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=32°.
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=32°.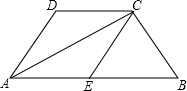 如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.