题目内容
7.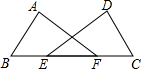 如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠A=∠D.
如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠A=∠D.
分析 先求出BF=CE,再利用“边边边”证明△ABF和△DCE全等,然后利用全等三角形对应角相等证明即可.
解答 证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
在△ABF和△DCE中,$\left\{\begin{array}{l}{BF=CE}\\{AB=DC}\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DCE(SSS),
∴∠A=∠D.
点评 本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法是解题的关键,难点在于求出BF=CE.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
15.下列几组数中,能构成直角三角形三边的是( )
| A. | 2,3,5 | B. | 3,4,4 | C. | 32,42,52 | D. | 9,12,15 |
2.在下列说法中,正确的是( )
| A. | 如果两个三角形全等,则它们一定能关于某直线成轴对称 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形的对称轴是底边上的高 | |
| D. | 若两个图形关于某直线对称,则它们的对应点一定位于对称轴的两侧 |

 如图,一条公路的转弯处是一段圆弧$\widehat{AB}$.
如图,一条公路的转弯处是一段圆弧$\widehat{AB}$.