题目内容
16. 如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
分析 (1)证明:连接OC,由PC是⊙O的切线,得到∠1+∠PCA=90°,由AB是⊙O的直径,得到∠2+∠B=90°,于是得到结论;
(2)当∠AOQ=∠AOC=50°时,△ABQ与△ABC的面积相等,求得点Q所经过的弧长=$\frac{50•π•6}{180}$=$\frac{5π}{3}$,当∠BOQ=∠AOC=50°时,即∠AOQ=130°时,△ABQ与△ABC的面积相等,求得点Q所经过的弧长=$\frac{130•π•6}{180}$=$\frac{13π}{3}$,当∠BOQ=50°时,即∠AOQ=230°时,△ABQ与△ABC的面积相等.
解答 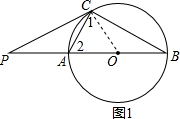 (1)证明:连接OC,
(1)证明:连接OC,
∵PC是⊙O的切线,
∴∠PCO=90°,
∴∠1+∠PCA=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠2+∠B=90°,
∵OC=OA,
∴∠1=∠2,
∴∠PCA=∠B;
(2)解:∵∠P=40°,
∴∠AOC=50°,
∵AB=12,
∴AO=6,
当∠AOQ=∠AOC=50°时,△ABQ与△ABC的面积相等,
∴点Q所经过的弧长=$\frac{50•π•6}{180}$=$\frac{5π}{3}$,
当∠BOQ=∠AOC=50°时,即∠AOQ=130°时,△ABQ与△ABC的面积相等,
∴点Q所经过的弧长=$\frac{130•π•6}{180}$=$\frac{13π}{3}$,
当∠BOQ=50°时,即∠AOQ=230°时,△ABQ与△ABC的面积相等,
∴点Q所经过的弧长=$\frac{230•π•6}{180}$=$\frac{23π}{3}$,
∴当△ABQ与△ABC的面积相等时,动点Q所经过的弧长为$\frac{5π}{3}$或$\frac{13π}{3}$或$\frac{23π}{3}$.
点评 本题考查了切线的性质,弦切角定理,弧长的求法,熟练掌握定理和计算公式是解题的关键.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在菱形ABCD中,AC=2,∠ABC=60°,则BD=2$\sqrt{3}$.
如图,在菱形ABCD中,AC=2,∠ABC=60°,则BD=2$\sqrt{3}$. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
 如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.
如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2). 兴的实际距离约为80km.
兴的实际距离约为80km.