题目内容
20.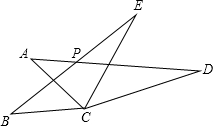 如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°.
如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°.
分析 (1)由条件可证明△ACD≌△BCE,根据全等三角形的性质得到∠ACB的度数;
(2)利用三角形内角和可求得∠APB=∠ACB,则可求得∠BPD.
解答 解:(1)在△ACD和△BCE中
$\left\{\begin{array}{l}{AC=BC}\\{AD=BE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE(SSS),
∴∠ACD=∠BCE,∠A=∠B,
∴∠BCA+∠ACE=∠ACE+∠ECD,
∴∠ACB=∠ECD=$\frac{1}{2}$(∠BCD-∠ACE)=$\frac{1}{2}$×(160°-80°)=40°;
(2)∵∠B+∠ACB=∠A+∠APB,
∴∠ABP=∠ACB=40°,
∴∠BPD=180°-40°=140°,
∴∠APB=180°-140°=40°,
故答案为:40°,40°.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
5.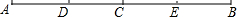 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
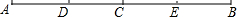 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )| A. | AC=2CE | B. | AB-AD=2CD | C. | AD=$\frac{1}{3}$DB | D. | DE=$\frac{1}{2}$AB |
10.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m与n的关系是( )
| A. | m+n=4 | B. | m+n=8 | C. | m=n=4 | D. | m=3,n=5 |
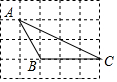 如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA=$\frac{3}{5}$.
如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA=$\frac{3}{5}$.