题目内容
9.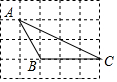 如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA=$\frac{3}{5}$.
如图,网格中的每一个正方形的边长都是1,△ABC的每一个顶点都在网格的交点处,则sinA=$\frac{3}{5}$.
分析 过B作BD垂直于AC,利用面积法求出BD的长,在直角三角形ABD中,利用锐角三角函数定义求出sinA的值即可.
解答  解:过点B作BD⊥AC,
解:过点B作BD⊥AC,
∵AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,BC=3,AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴S△ABC=$\frac{1}{2}$×3×2=$\frac{1}{2}$×2$\sqrt{5}$×BD,
解得:BD=$\frac{3\sqrt{5}}{5}$,
在Rt△ABD中,sinA=$\frac{BD}{AB}$=$\frac{\frac{3\sqrt{5}}{5}}{\sqrt{5}}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$
点评 此题考查了锐角三角函数定义,勾股定理,以及三角形面积公式,牢记锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
4.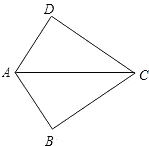 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BAC=∠DAC | ||
| C. | ∠BCA=∠DCA | D. | ∠B=∠D=90°,∠DAC=56°,∠BCA=34° |
1.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a3)2=a6 | C. | a3•a2=a6 | D. | a8÷a4=a2 |
18.2017的倒数是( )
| A. | $\frac{1}{2017}$ | B. | -$\frac{1}{2017}$ | C. | 2017 | D. | -2017 |
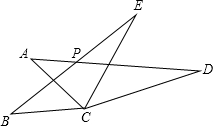 如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°.
如图,△ACD与△BCE中,AC=BC,AD=BE,CD=CE,若∠ACE=80°,∠BCD=160°,AD与BE相交于P点,则∠ACB的度数为40°,∠APB的度数为40°. 如图,点O是直线AB上一点,∠DOF=90°,OC平分∠AOD,OE平分∠BOF,∠EOF=20°,求∠AOC的度数.
如图,点O是直线AB上一点,∠DOF=90°,OC平分∠AOD,OE平分∠BOF,∠EOF=20°,求∠AOC的度数.