题目内容
17．
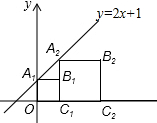正方形A1B1C1O和正方形A2B2C2C1按如图所示方式放置，A1、A2在直线y=2x+1上，点C1，C2在x轴上，已知A1点的坐标是（0，1），则点B2的坐标为（4，3）．
分析 根据正方形的性质以及点A1的坐标即可得出OC1的长度，将x=1代入y=2x+1中求出y值，再根据正方形的性质即可得出C1C2=B2C2=3，由此即可得出点B2的坐标．
解答 解：∵A1点的坐标是（0，1），四边形A1B1C1O为正方形，
∴OC1=1，
令y=2x+1中x=1，则y=3，
∴C1A2=3，
∵四边形A2B2C2C1为正方形，
∴C1C2=B2C2=3，
∴OC2=OC1+C1C2=4，
∴点B2的坐标为（4，3）．
故答案为：（4，3）．
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质，解题的关键是求出线段OC1、C1C2、B2C2的长度．本题属于基础题，难度不大，解决该题型题目时，根据正方形的性质找出边的长度是关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
9．2x3可以表示为（ ）
| A． | x3+x3 | B． | x3•x3 | C． | 2x•2x•2x | D． | 8x |
9．
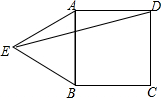如图，点E是正方形ABCD外一点，EA=4，EB=3，且∠AEB=45°，则ED的长为（ ）
如图，点E是正方形ABCD外一点，EA=4，EB=3，且∠AEB=45°，则ED的长为（ ）| A． | $\sqrt{23}$ | B． | 2$\sqrt{10}$ | C． | $\sqrt{41}$ | D． | 5$\sqrt{2}$ |
12．下列各式中，同学们的计算结果不正确的是（ ）
| A． | $\sqrt{5}×\sqrt{7}$=2$\sqrt{3}$ | B． | $\sqrt{6}÷\sqrt{3}$=$\sqrt{2}$ | C． | $\sqrt{\frac{1}{10}}$×$\sqrt{8}$=$\frac{2\sqrt{5}}{5}$ | D． | $\sqrt{\frac{4}{7}}$÷$\sqrt{\frac{7}{4}}$=$\frac{4}{7}$ |
9．
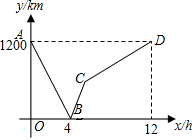如图所示，一列列车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km）图中的折线表示y与x之间的函数关系，下列说法中错误的是（ ）
如图所示，一列列车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km）图中的折线表示y与x之间的函数关系，下列说法中错误的是（ ）| A． | B点表示快车与慢车出发4小时两车相遇 | |
| B． | B-C-D段表示慢车先加速后减速最后到达甲地 | |
| C． | 快车的速度为200km/h | |
| D． | 慢车的速度为100km/h |