题目内容
3.已知关于x的一元二次方程x2+4x-k=0有两个不相等的实数根.(1)求k的取值范围;
(2)请你在-5,-4,-3,1,2,3中选择一个数作为k的值,使方程有两个整数根,并求出方程的两个整数根.
分析 (1)根据方程有两个不等实根结合根的判别式,可得出关于k的一元一次不等式,解不等式即可得出k的取值范围;
(2)结合(1)的结论,找出k的值,并验证k为这些数时,何时方程的两根为整数,由此即可得出结论.
解答 解:(1)∵方程x2+4x-k=0有两个不相等的实数根,
∴△=42-4×1×(-k)=16+4k>0,
解得:k>-4,
∴k的取值范围为k>-4;
(2)当k=-3时,△=16+4k=4,
原方程为x2+4x+3=(x+1)(x+3)=0,
解得:x=-1或x=-3;
当k=1时,△=16+4k=20,
$\sqrt{20}$不是整数;
当k=2时,△=16+4k=24,
$\sqrt{24}$不是整数;
当k=3时,△=16+4k=28,
$\sqrt{28}$不是整数.
∴当取k=-3时,方程的两个整数根为-1或-3.
点评 本题考查了根的判别式以及解一元一次不等式,解题的关键是:(1)找出△=16+4k>0;(2)验证k为何值时,方程有两个整数根.本题属于中档题,难度不大,解决该题型题目时,根据方程根的个数结合根的判别式得出不等式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
13. 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )| A. | $\sqrt{17}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2 |
14.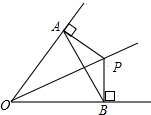 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )| A. | PA=PB | B. | OA=OB | C. | PO平分∠APB | D. | AB垂直平分OP |
18. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=30°,则∠OCB的度数为( )| A. | 30° | B. | 60° | C. | 50° | D. | 40° |
8.公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
表二:
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
(Ⅰ)设租用甲种货车x辆(x为非负整数),试填写表格.
表一:
| 租用甲种货车的数量/辆 | 3 | 7 | x |
| 租用的甲种货车最多运送机器的数量/台 | 135 | 315 | 45x |
| 租用的乙种货车最多运送机器的数量/台 | 150 | 30 | -30x+240 |
| 租用甲种货车的数量/辆 | 3 | 7 | x |
| 租用甲种货车的费用/元 | 1200 | 2800 | 400x |
| 租用乙种货车的费用/元 | 1400 | 280 | -280x+2240 |
15. 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
12.下列各组数中,不能构成直角三角形的是( )
| A. | 2,3,4 | B. | 5,12,13 | C. | 6,8,10 | D. | 3,4,5 |