题目内容
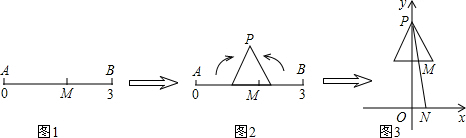
在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1,将AB折成正三角形,使点A、B重合于点P,如图2,建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m=1.8时,求n的值.

考点:相似三角形的判定与性质,实数与数轴,等边三角形的性质,平移的性质
专题:常规题型
分析:易证△PFM∽△PON,根据相似三角形对应边比例相等可得
=
,即可解题.
| PF |
| OP |
| FM |
| ON |
解答:解:如图

∵AB=3,△PDE是等边三角形,
∴PD=PE=DE=1,
以DE的垂直平分线为y轴建立直角坐标系,
∵△PDE关于y轴对称,
∴PF⊥DE,DF=EF,DE∥x轴,
∴PF=
,
∴△PFM∽△PON,
∵m=
,
∴FM=
-
,
∴
=
,即
=
,
解得ON=4-2
.

∵AB=3,△PDE是等边三角形,
∴PD=PE=DE=1,
以DE的垂直平分线为y轴建立直角坐标系,
∵△PDE关于y轴对称,
∴PF⊥DE,DF=EF,DE∥x轴,
∴PF=
| ||
| 2 |
∴△PFM∽△PON,
∵m=
| 3 |
∴FM=
| 3 |
| 3 |
| 2 |
∴
| PF |
| OP |
| FM |
| ON |
| ||||
| 2 |
| ||||
| ON |
解得ON=4-2
| 3 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质.

练习册系列答案
相关题目
中石油年输油量1500万吨,用科学记数法表示1500万吨正确的是( )
| A、1.5×107万吨 |
| B、1.5×103万吨 |
| C、15×102万吨 |
| D、0.15×104万吨 |
 如图,将连续的奇数1、3、5、7 …,排列成如下的数表,用十字框框出5个数.问:
如图,将连续的奇数1、3、5、7 …,排列成如下的数表,用十字框框出5个数.问: 尺规作图:(保留作图痕迹,不写作法)已知:如图,线段m,n,∠α.求作:△ABC,使得∠A=∠α,AB=m,AC=n.
尺规作图:(保留作图痕迹,不写作法)已知:如图,线段m,n,∠α.求作:△ABC,使得∠A=∠α,AB=m,AC=n. 如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.
如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.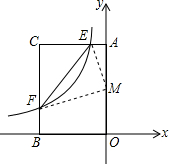 如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=
如图,在平面直角坐标系xOy中,矩形AOBC的AO边在y轴上,BO边在x轴上,C点坐标为(-2,3),反比例函数y=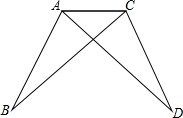 如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,AD=BC,请说明∠B=∠D的道理,小明动手测量了一下,发现∠B确实与∠D相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.
如图,小明在完成数学作业时,遇到了这样一个问题,AB=CD,AD=BC,请说明∠B=∠D的道理,小明动手测量了一下,发现∠B确实与∠D相等,但他不能说明其中的道理,你能帮助他说明这个道理吗?试试看.