题目内容
在一个等腰直角三角形的内部作一个矩形ABCD，其中等腰直角三角形的腰长为20cm，求矩形ABCD面积的最大值．
考点：相似三角形的判定与性质,二次函数的最值,等腰直角三角形
专题：常规题型
分析：设矩形的一条边长是x，面积是y，另一边就是20-x，利用矩形面积即可得到关于边长x的二次函数的解析式计算即可
解答：解：如图，
∵AB∥CD，
∴AB+BC=20，
设矩形的一条边长是x，另一边就是20-x，设矩形的面积为y
∴y=x（20-x），
y=-x2+20x=-（x-10）2+100（0＜x＜20），
∴x=10时，y有最大值100．
则矩形的最大面积为100cm2．
∵AB∥CD，
∴AB+BC=20，
设矩形的一条边长是x，另一边就是20-x，设矩形的面积为y
∴y=x（20-x），
y=-x2+20x=-（x-10）2+100（0＜x＜20），
∴x=10时，y有最大值100．
则矩形的最大面积为100cm2．
点评：本题考查了函数式的最值问题，考查了相似三角形的判定和相似三角形对应边比例相等的性质．
练习册系列答案
相关题目
如果|a|=a，下列各式成立的是（ ）
| A、a＞0 | B、a＜0 |
| C、a≥0 | D、a≤0 |
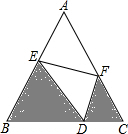如图，已知D为BC上一点，∠B=∠C=∠EDF=60°，BE=6，CD=3，CF=4，求AF的长．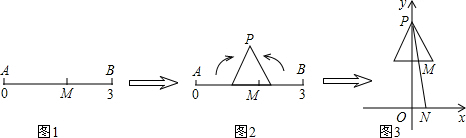
利用网格线作图：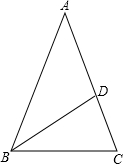
如图，在△ABC中，AB=AC，BD平分∠ABC，若∠BDC=84°．求∠A的度数．