题目内容
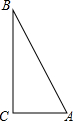 如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.
如图,△ABC是直角三角形,∠ACB=90°,在△ABC内剪出一块半圆,使圆心在BC边上,且半圆的弧与边AB相切.(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(2)若AC=5,BC=12,求⊙O的半径.
考点:作图—复杂作图
专题:
分析:(1)利用角平分线的性质进而得出答案;
(2)利用切线的性质以及勾股定理进而求出即可.
(2)利用切线的性质以及勾股定理进而求出即可.
解答: 解:(1)如图所示:半圆O即为所求;
解:(1)如图所示:半圆O即为所求;
(2)∵∠ACB=90°,AC=5,BC=12,
∴AB=13,
设半圆O与AB相切于点E,连接EO,
设CO=x,则EO=x,
则BO=12-x,BE=13-5=8,
故在Rt△ABC中
BO2=BE2+EO2,
则(12-x)2=82+x2,
解得:x=
,
即⊙O的半径为
.
 解:(1)如图所示:半圆O即为所求;
解:(1)如图所示:半圆O即为所求;(2)∵∠ACB=90°,AC=5,BC=12,
∴AB=13,
设半圆O与AB相切于点E,连接EO,
设CO=x,则EO=x,
则BO=12-x,BE=13-5=8,
故在Rt△ABC中
BO2=BE2+EO2,
则(12-x)2=82+x2,
解得:x=
| 10 |
| 3 |
即⊙O的半径为
| 10 |
| 3 |
点评:此题主要考查了复杂作图以及勾股定理,熟练应用勾股定理是解题关键.

练习册系列答案
相关题目
若1<x<2,则|1-x|+|x-2|等于( )
| A、2x-3 | B、-1 |
| C、1 | D、3-2x |
 利用网格线作图:
利用网格线作图: 如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.
如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求:AF、BD、CF的长.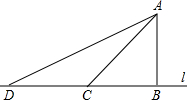 校车安全是当今社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度实验:先在公路旁边选取一点A,再在笔直的车道L上确定点B,使AB与L垂直,测得AB=21米,在L上点B的同侧取点C、D,使∠ADB=30°,∠ACB=60°.
校车安全是当今社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度实验:先在公路旁边选取一点A,再在笔直的车道L上确定点B,使AB与L垂直,测得AB=21米,在L上点B的同侧取点C、D,使∠ADB=30°,∠ACB=60°.