题目内容
10.阅读下面的材料,并完成填空: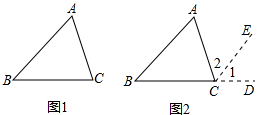
如图1,在△ABC中,试说明∠A+∠B+∠C=180°.
分析:通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角.
解:如图2,延长BC到点D,过点C作CE∥AB.
∵CE∥AB(已作),
∴∠B=∠2,(两直线平行,同位角相等)
∠A=∠1,两直线平行,内错角相等.
∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠C=180°等量代换.
分析 根据平行线的性质以及各角度的位置关系填空即可.
解答 解:如图2,延长BC到点D,过点C作CE∥AB.
∵CE∥AB(已作),
∴∠B=∠2,(两直线平行,同位角相等)
∠A=∠1,(两直线平行,内错角相等).
∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠C=180°(等量代换).
故答案为:∠2; 两直线平行,内错角相等;等量代换.
点评 本题考查了利用平行线的性质以及平角等于180°求证三角形的内角和定理,熟练掌握平行线的性质并准确识图是解题的关键.

练习册系列答案
相关题目
2.下列结论中正确的是( )
| A. | 正数、负数统称为有理数 | B. | 无限小数都是无理数 | ||
| C. | 有理数、无理数统称为实数 | D. | 两个无理数的和一定是无理数 |
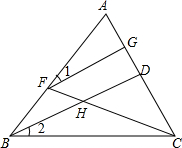 如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.
如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.