题目内容
13. 如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.
如图,△ABC中,AB=AC,D点在BC上,∠BAD=30°,且∠ADC=60°.请完整说明为何AD=BD与CD=2BD的理由.
分析 求出∠B、∠C、∠DAC的度数,根据等腰三角形的判定方法以及30度直角三角形的性质即可解决问题.
解答 解:∵∠4=60°,∠1=30°,
根据三角形外角定理可得:∠ABD=∠4-∠1=60°-30°=30°=∠1.
∴BD=AD.
∵∠ABD=30°,
又∵AB=AC,
∴∠C=∠ABD=30°,
∴∠2=180°-∠4-∠C=180°-60°-30°=90°,
∵∠C=30°,
∴CD=2AD=2BD.
点评 本题考查等腰三角形的判定和性质、直角三角形30度角性质等知识,解题的关键是灵活应用这些知识解决问题,属于基础题,中考常考题型.

练习册系列答案
相关题目
8.有一种病毒呈球形,其最小直径约为0.000 000 08米,用科学记数法表示为( )
| A. | 80×10-9米 | B. | 0.8×10-7米 | C. | 8×10-8米 | D. | 8×10-9米 |
18.下列计算正确的是( )
| A. | (x2)3=x6 | B. | x2•x3=x6 | C. | x2+x3=x5 | D. | x6÷x3=x2 |
5.进入春季后,杨树、柳树飞絮影响着人们的生活,本市将对现有的2000000棵杨、柳树雌株进行治理,减少飞絮现象.将2000000用科学记数法表示为( )
| A. | 2×107 | B. | 2×106 | C. | 20×105 | D. | 200×104 |
2.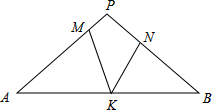 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 88° | D. | 92° |
3.门头沟位于北京西南部,属太行山余脉,地势险要“东望都邑,西走塞上而通大漠”,自古为兵家必争之地,全区总面积1455平方公里,其中山区占98.5%.将数字1455用科学记数法表示为( )
| A. | 1.455×103 | B. | 14.55×102 | C. | 1.455×104 | D. | 0.1455×104 |
 如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).
如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).