题目内容
15.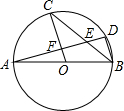 如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )
如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.若∠CBD=36°,则下列结论中不正确的是( )| A. | ∠AOC=72° | B. | ∠AEC=72° | C. | AF=DF | D. | BD=20F |
分析 根据直径的性质以及平行线的性质可知OC⊥AD,由此可以推出A、C、D正确,B错误.
解答  解:∵AB是直径,
解:∵AB是直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AFO=∠ADB=90°,
∴OC⊥AD,
∴AF=DF,故C正确,
∵OB=OC,∠CBD=36°,
∴∠C=∠CBO=∠CBD=36°,
∴∠AOC=∠C+∠CBO=72°,故A正确,
∵AO=OB,AF=FD,
∴BD=2OF,故D正确,
∵∠AEC=90°-∠C=54°,故B错误,
故选B.
点评 本题考查圆周角定理、直径的性质、平行线的性质、垂径定理等知识,灵活运用这些知识是解决问题的关键,属于基础题,中考常考题型.

练习册系列答案
相关题目
6.已知一组数据:10,8,10,8,6,13,11,10,12,9,11,12,9,10,11,10,7,8,12,9,那么频率为0.2的范围是( )
| A. | 5.5~7.5 | B. | 7.5~9.5 | C. | 9.5~11.5 | D. | 11.5~13.5 |
10.已知3n+3=(9n)2,则n等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.(x2-mx+1)(x-1)的积中x的二次项系数为零,则m的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
7.已知三角形斜边的长是8,则斜边上的中线长为( )
| A. | 16 | B. | 12 | C. | 4 | D. | 2 |
5.进入春季后,杨树、柳树飞絮影响着人们的生活,本市将对现有的2000000棵杨、柳树雌株进行治理,减少飞絮现象.将2000000用科学记数法表示为( )
| A. | 2×107 | B. | 2×106 | C. | 20×105 | D. | 200×104 |
 如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).
如图,一游人由山脚A沿坡角为30°的山坡AB行走600m,到达一个景点B,再由B沿山坡BC行走200m到达山顶C,若在山顶C处观测到景点B的俯角为45°,则山高CD=300+100$\sqrt{2}$m(结果用根号表示).