如图所示.线段AC的垂直平分线交线段AB于点D.∠A=50°.则∠BDC=( )A．50°B．100°C．120°D．130° 题目和参考答案——青夏教育精英家教网—

题目内容

6．

如图所示，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（　　）

A．

50°

B．

100°

C．

120°

D．

130°

分析根据线段垂直平分线的性质得到DA=DC，根据等腰三角形的性质得到∠DCA=∠A，根据三角形的外角的性质计算即可．

解答解：∵DE是线段AC的垂直平分线，
∴DA=DC，
∴∠DCA=∠A=50°，
∴∠BDC=∠DCA+∠A=100°，
故选：B．

点评本题考查的是线段垂直平分线的性质和三角形的外角的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

练习册系列答案

魔法教程课本诠释与思维拓展训练系列答案

北京市小学毕业考试考试说明系列答案

晨读晚练系列答案

相关题目

16．下列图形中，是轴对称图形但不是中心对称图形的是（　　）

17．

如图，直线CD∥BF，直线AB与CD、EF分别相交于点M、N，若∠1=30°，则∠2=30°．

14．

如图，已知直线a∥b，∠1=100°，则∠2等于（　　）

1．解不等式组，并把解集在数轴上表示出来．
$\left\{\begin{array}{l}{2x+1≥0}\\{\frac{x+5}{3}-\frac{x}{2}＞1}\end{array}\right.$．

11．

如图所示，一只蚂蚁从A点出发到D，E，F处寻觅食物．假定蚂蚁在每个岔路口都等可能的随机选择一条向左下或右下的路径（比如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口）．那么，蚂蚁从A出发到达E处的概率是$\frac{1}{2}$．

18．

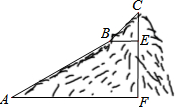如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．
（1）求AB段山坡的高度EF；
（2）求山峰的高度CF．（$\sqrt{2}≈$1.414，CF结果精确到米）

15．计算：|$\sqrt{3}-\sqrt{2}$|+（$\sqrt{2015}-1$）⁰+2sin45°-2cos30°+（$\frac{1}{2015}$）^-1．

4．分式$\frac{1}{x-2}$有意义，则x的取值范围是（　　）

试题分类