题目内容
16.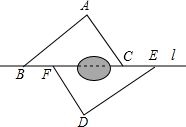 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
分析 (1)先证明BC=EF,再根据SSS即可证明.
(2)结论AB∥DE,AC∥DF,根据全等三角形的性质即可证明.
解答  (1)证明:∵BF=CE,
(1)证明:∵BF=CE,
∴BF+FC=FC+CE,即BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SSS).
(2)结论:AB∥DE,AC∥DF.
理由:∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,
∴AB∥DE,AC∥DF.
点评 本题考查全等三角形的判定和性质、平行线的判定等知识,解题的关键是正确寻找全等三角形的条件,记住平行线的判定方法,属于基础题,中考常考题型.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
6. 如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于( )
如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于( )
 如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于( )
如图,正三角形ABC内接于圆O,AD⊥BC于点D交圆于点E,动点P在优弧BAC上,且不与点B,点C重合,则∠BPE等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
8.已知关于x的一元二次方程x2+mx-8=0的一个实数根为2,则另一实数根及m的值分别为( )
| A. | 4,-2 | B. | -4,-2 | C. | 4,2 | D. | -4,2 |
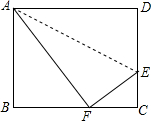 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么矩形ABCD的周长为36cm.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5$\sqrt{5}$cm,且tan∠EFC=$\frac{3}{4}$,那么矩形ABCD的周长为36cm. 小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°,由此可知三角板的较短直角边的长度约为9cm.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
小聪有一块含有30°角的直角三角板,他想只利用量角器来测量较短直角边的长度,于是他采用如图的方法,小聪发现点A处的三角板读数为12cm,点B处的量角器的读数为74°,由此可知三角板的较短直角边的长度约为9cm.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)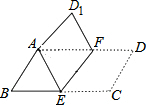 如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD=55°.
如图,把平行四边形ABCD折叠,使点C与点A重合,这时点D落在D1,折痕为EF,若∠BAE=55°,则∠D1AD=55°.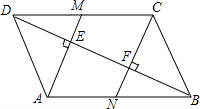 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.