题目内容
20．已知等腰三角形两边a，b，满足a2+b2-4a-10b+29=0，则此等腰三角形的周长为（ ）| A． | 9 | B． | 10 | C． | 12 | D． | 9或12 |
分析 先运用分组分解法进行因式分解，求出a，b的值，再代入求值即可．
解答 解：∵a2+b2-4a-10b+29=0，
∴（a2-4a+4）+（b2-10b+25）=0，
∴（a-2）2+（b-5）2=0，
∴a=2，b=5，
∴当腰为5时，等腰三角形的周长为5+5+2=12，
当腰为2时，2+2＜5，构不成三角形．
故选：C．
点评 此题考查了配方法的应用，三角形三边关系及等腰三角形的性质，解题的关键熟练掌握完全平方公式．
练习册系列答案
相关题目
8．已知a是方程x2+x-2015=0的一个根，则$\frac{2}{{{a^2}-1}}-\frac{1}{{{a^2}-a}}$的值为（ ）
| A． | 2014 | B． | 2015 | C． | $\frac{1}{2014}$ | D． | $\frac{1}{2015}$ |
15．下列运算中正确的是（ ）
| A． | （a2）3=a5 | B． | a5+a5=2a10 | C． | a6÷a2=a3 | D． | a4•a5=a9 |
△ABC在平面直角坐标系中的位置如图所示，点A（-2，2），点B（-3，-1），点C（-1，1）．
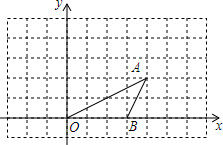在边长为1的方格纸中建立直角坐标系，如图所示，O、A、B三点均为格点．
已知 a、b、c三数在数轴上的位置如图所示，其中|a|=|c|，化简：$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+|c|-|a|．