题目内容
8．
如图，D、E分别是BC、AC的中点，BF平分∠ABC交DE于点F，若BC=6，AB=8，则EF的长是1．
分析 根据三角形中位线定理得到DE∥AB，DE=$\frac{1}{2}$AB=4，根据平行线的性质、角平分线的定义求出DF，计算即可．
解答 解：∵D、E分别是BC、AC的中点，
∴DE∥AB，DE=$\frac{1}{2}$AB=4，BD=$\frac{1}{2}$BC=3，
∴∠ABF=∠BFD，
∵BF平分∠ABC，
∴∠ABF=∠DBF，
∴∠DBF=∠BFD，
∴DF=DB=3，
∴EF=DE-DF=1．
故答案是：1．
点评 本题考查的是角平分线的定义、三角形中位线定理，掌握平行线的性质、角平分线的定义是解题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
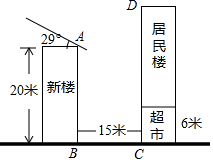某居民小区有一朝向为正南方向的居民楼．该居民楼的一楼是高6米的小区超市，超市以上是居民住房．在该楼前面15米处要盖一栋高20米的新楼．已知上海地区冬至正午的阳光与水平线夹角为29°．（参考数据：sin29°≈0.48；cos29°≈0.87；tan29°≈0.55）
19．已知a，b，c，d为有理数，现规定一种新的运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，那么当$|\begin{array}{l}{2}&{4}\\{（1-x）}&{5x}\end{array}|$=18时，则x的值是（ ）
| A． | x=1 | B． | $x=\frac{7}{11}$ | C． | $x=\frac{11}{7}$ | D． | x=-1 |
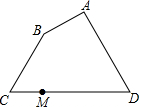如图，
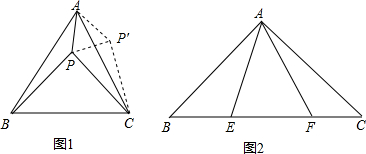
在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是以点A为圆心4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为7．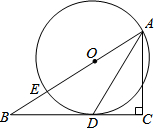
如图，在△ABC中，∠C=90°，点E在AB上，以AE为直径的⊙O与BC相切于点D，连接AD．