题目内容
9.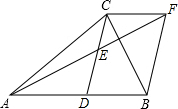 如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.
如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.(1)求证:DB=CF;
(2)若AC=BC,求证:BDCF为矩形;
(3)在(2)的情况下,若∠ABC=60°,AB=2,求BDCF的面积.
分析 (1)由SAS证明△AED≌△FEC,得出对应边相等AD=CF.再由DB=AD,即可得出结论.
(2)由全等三角形的性质得出∠ADE=∠FCE,证出DB∥CF,得出四边形BDCF是平行四边形,再由等腰三角形的三线合一性质得出CD⊥AB.即可得出结论;
(3)证明△ABC是等边三角形,DB=$\frac{1}{2}$AB=1,得出BC=2DB=2,由勾股定理求出CD,即可得出四边形的面积.
解答 (1)证明:∵CD是AB边的中线,E是CD中点,
∴AD=DB,DE=CE,
在△AED和△FEC中,$\left\{\begin{array}{l}{AE=EF}&{\;}\\{∠AED=∠FEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△AED≌△FEC(SAS).
∴AD=CF.
∵DB=AD,
∴DB=CF.
(2)解:由(1)得:△AED≌△FEC,
∴∠ADE=∠FCE,
∴DB∥CF,
∵DB=CF,
∴四边形BDCF是平行四边形,
∵AC=BC,D是AB的中点,
∴CD⊥AB.
∴∠CDB=90°,
∴四边形BDCF是矩形.
(3)解:∵∠ABC=60°,AB=2,AC=BC,
∴△ABC是等边三角形,DB=$\frac{1}{2}$AB=1,
∴BC=2DB=2,
∴CD=$\sqrt{B{C}^{2}-D{B}^{2}}$=$\sqrt{3}$,
∴四边形BDCF的面积=DB•CD=1×$\sqrt{3}$=$\sqrt{3}$.
点评 本题考查了全等三角形的判定与性质、矩形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、勾股定理等知识;本题综合性强,证明三角形全等是解决问题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
14.若圆的一条弦把圆分成度数比为1:4的两段弧,则弦所对的圆周角等于( )
| A. | 36° | B. | 72° | C. | 36°或144° | D. | 72°或108° |
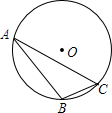 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.
如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π. 已知a,b两数在数轴上的表示如图所示,则-a>b.(填“>”、“=”或“<”)
已知a,b两数在数轴上的表示如图所示,则-a>b.(填“>”、“=”或“<”)