题目内容
4.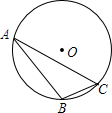 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.
如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.
分析 连OB,OC,根据圆周角定理得到∠BOC=2∠BAC=72°,弦BC所对的弧分为优弧和劣弧,然后根据弧长公式计算弧BC的长,故有两个答案.
解答 解:连OB,OC,如图, ∵∠BAC=36°,
∵∠BAC=36°,
∴∠BOC=2∠BAC=72°,
∴劣弧$\widehat{BC}$=$\frac{72•π•1}{180}$=$\frac{2}{5}$π;
优弧$\widehat{BC}$=$\frac{268•π•1}{180}$=$\frac{8}{5}$π.
故答案为$\frac{2}{5}$π或$\frac{8}{5}$π.
点评 本题考查了弧长公式:l=$\frac{nπr}{180}$,也考查了圆周角定理,掌握弧长公式和圆周角定理是解题的关键.

练习册系列答案
相关题目
6.计算$\sqrt{2013×2014×2015×2016+1}$-20142=( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
14.为了完成下列任务,你认为采用普查方式较为合适的是( )
| A. | 了解一批苹果是否甜 | |
| B. | 调查深圳学生的“垃圾减量分类”的意识 | |
| C. | 检测某种汽车的发动机性能 | |
| D. | 测算某校某班学生平均身高 |


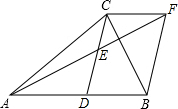 如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.
如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF. 在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)
在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留一位小数)