题目内容
14.若圆的一条弦把圆分成度数比为1:4的两段弧,则弦所对的圆周角等于( )| A. | 36° | B. | 72° | C. | 36°或144° | D. | 72°或108° |
分析 圆的一条弦把圆分成度数之比为1:4的两条弧,则所分的劣弧的度数是72°,当圆周角的顶点在优弧上时,这条弦所对的圆周角等于36°,当这条弦所对的圆周角的顶点在劣弧上时,这条弦所对的圆周角等于144°;即可得出结果.
解答  解:如图所示,弦AB将⊙O分成了度数比为1:4两条弧.
解:如图所示,弦AB将⊙O分成了度数比为1:4两条弧.
连接OA、OB;
则∠AOB=$\frac{1}{5}$×360°=72°;
①当所求的圆周角顶点位于D点时,
这条弦所对的圆周角∠ADB=$\frac{1}{2}$∠AOB=36°;
②当所求的圆周角顶点位于C点时,
这条弦所对的圆周角∠ACB=180°-∠ADB=144°.
故选:C.
点评 本题考查了圆心角、弧、弦的关系及圆周角定理;在解答此类问题时要注意是在“同圆或等圆中”才适用,这是此类问题的易错点.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
19.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
 如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
4.下列各数中,没有平方根的是( )
| A. | -4 | B. | 0 | C. | 0.25 | D. | $\sqrt{2}$ |


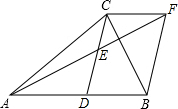 如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.
如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.