题目内容
18.将一个矩形沿着一条对称轴翻折,如果所得到的矩形与这个矩形相似,那么我们就将这样的矩形定义为“白银矩形”.事实上,“白银矩形”在日常生活中随处可见.如,我们常见的A4纸就是一个“白银矩形”.请根据上述信息求A4纸的较长边与较短边的比值.这个比值是$\sqrt{2}$.分析 根据相似多边形的对应边的比相等列出比例式,计算即可.
解答 解: 由题意得,四边形ABFE∽四边形ADCB,
由题意得,四边形ABFE∽四边形ADCB,
∴$\frac{AB}{AD}$=$\frac{AE}{AB}$,
∴AB2=$\frac{A{D}^{2}}{2}$,
∴$\frac{AD}{AB}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边的比相等、对应角相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
 如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA到D,则∠CAD的度数为( )| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
7.下列每组中的两个单项式,属于同类项的是( )
| A. | 2a与-3a2 | B. | -ab与$\frac{2ab}{3}$ | C. | 3abc与-2ab | D. | $\frac{1}{2}$a2b与ab2 |
 的解是负数,则m的取值范围是______.
的解是负数,则m的取值范围是______.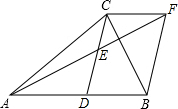 如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.
如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.