题目内容
14. 已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°经过5次翻转之后,点B的坐标是($\frac{11}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°经过5次翻转之后,点B的坐标是($\frac{11}{2}$,$\frac{\sqrt{3}}{2}$).
分析 根据正六边形的性质,求出5次翻转前进的距离=1×5=5,过点B作BG⊥x于G,求出∠BAG=60°,然后求出AG、BG,再求出OG,然后写出点B的坐标即可.
解答  解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,A(-1,0),
解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,A(-1,0),
∴AB=1,
∴翻转前进的距离=1×5=5,
如图,过点B作BG⊥x于G,则∠BAG=60°,
∴AG=1×$\frac{1}{2}$=$\frac{1}{2}$,BG=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴OG=5+$\frac{1}{2}$=$\frac{11}{2}$,
∴点B的坐标为($\frac{11}{2}$,$\frac{\sqrt{3}}{2}$).
故答案为:($\frac{11}{2}$,$\frac{\sqrt{3}}{2}$).
点评 本题考查了坐标与图形变化-旋转,正六边形的性质,确定出最后点B所在的位置是解题的关键,难点在于作辅助线构造出直角三角形.

练习册系列答案
相关题目
4.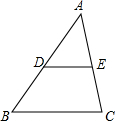 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
 如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )
如图,已知在△ABC中,DE∥BC,BC=6,ED=2,点A到BC的距离为5,则A到DE的距离是( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
3.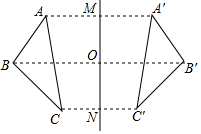 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
 如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )| A. | AC=A′C′ | B. | BO=B′O | C. | AA′⊥MN | D. | AB∥B′C′ |
4.某射击运动员进行两次射击(每次射击成绩最小环数是0环,最大环数是10环),则下列说法中正确的是( )
| A. | “该运动员两次的射击成绩都是9环”属于随机事件 | |
| B. | “该运动员一次的射击成绩为10环,一次的射击成绩为0环”属于不可能事件 | |
| C. | “该运动员两次的射击成绩的总成绩为21环”属于必然事件 | |
| D. | 该运动员一次的射击成绩大于6环的可能性比大于8环的可能性小 |
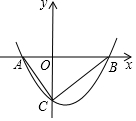 平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.
平面直角坐标系中,将抛物线y=ax2经平移后与x轴交于点A、B,与y轴交于点C,若$\frac{{{S_{△AOC}}}}{{{S_{△BOC}}}}=\frac{{\sqrt{5}-1}}{2}$,则称平移后的抛物线所在的位置为抛物线y=ax2在该平面直角坐标系中的一个“黄金位”.如图所示的抛物线为抛物线y=ax2的一个“黄金位”,且AB=2,将图中的抛物线向右平移$\frac{5+\sqrt{5}}{2}$个单位长度又可得到抛物线y=ax2的另一个“黄金位”.