题目内容
15.解下列方程组:(1)$\left\{\begin{array}{l}x+2y=1\\ 3x-2y=11\end{array}\right.$
(2)$\left\{\begin{array}{l}3x+2y=5\\ 2x+5y=7\end{array}\right.$
(3)$\left\{\begin{array}{l}3x+2y=-1\\ 3(y+2)=3-2x\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=1①}\\{3x-2y=11②}\end{array}\right.$,
①+②得:4x=12,
解得:x=3,
把x=3代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+2y=5①}\\{2x+5y=7②}\end{array}\right.$,
①×2-②×3得:-11y=-11,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为$\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{3x+2y=-1①}\\{2x+3y=-3②}\end{array}\right.$,
①×3-②×2得:5x=3,
解得:x=$\frac{3}{5}$,
把x=$\frac{3}{5}$代入①得:y=-$\frac{7}{5}$,
则方程组的解为$\left\{\begin{array}{l}x=\frac{3}{5}\\ y=-\frac{7}{5}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
4.若7<$\sqrt{a}$<8,则a的值可以是( )
| A. | 49 | B. | 59 | C. | 69 | D. | 79 |
5. 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )| A. | ($\frac{\sqrt{3}}{2}$)2016 | B. | ($\sqrt{3}$)2016 | C. | 22017 | D. | ($\sqrt{3}$)2017 |
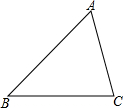 为落实中央提出绿色发展的理念,某环保部门对A、B、C三个企业的污水进行集中处理,计划在道路AB上建立一个污水处理站D,使得到这三个企业铺设的污水管道总长度最短.已知∠ABC=45°,∠ACB=75°,AC=20千米,在图中画出污水处理站D的位置,并求所铺设的管道总长度(结果保留根号).
为落实中央提出绿色发展的理念,某环保部门对A、B、C三个企业的污水进行集中处理,计划在道路AB上建立一个污水处理站D,使得到这三个企业铺设的污水管道总长度最短.已知∠ABC=45°,∠ACB=75°,AC=20千米,在图中画出污水处理站D的位置,并求所铺设的管道总长度(结果保留根号). 如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6$\sqrt{3}$米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6$\sqrt{3}$米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).