题目内容
6．解方程组：$\left\{\begin{array}{l}{{x}^{2}-4xy+{3y}^{2}=0①}\\{2x+y=21②}\end{array}\right.$．分析 把①变形得出x-3y=0，x-y=0，则原方程组化为两个二元一次方程组，求出方程组的解即可．
解答 解：由①得：（x-3y）（x-y）=0，
x-3y=0，x-y=0，
则原方程组化为：$\left\{\begin{array}{l}{x-3y=0}\\{2x+y=21}\end{array}\right.$或$\left\{\begin{array}{l}{x-y=0}\\{2x+y=21}\end{array}\right.$
解得：$\left\{\begin{array}{l}{{x}_{1}=9}\\{{y}_{1}=3}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=7}\\{{y}_{2}=7}\end{array}\right.$
∴原方程组的解为：$\left\{\begin{array}{l}{{x}_{1}=9}\\{{y}_{1}=3}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=7}\\{{y}_{2}=7}\end{array}\right.$．
点评 本题考查了高次方程组，能把高次方程组转化成二元一次方程组是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
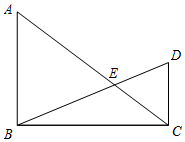已知：如图，在Rt△ABC和Rt△BCD中，∠ABC=∠BCD=90°，BD与AC相交于点E，AB=9，cos∠BAC=$\frac{3}{5}$，tan∠DBC=$\frac{5}{12}$．
如图，将平行四边形ABCD的边DC延长到点E，使CE=DC，连结AE，交BC于点F，连结AC、BE．
如图，点A的坐标为（-5，0），直线y=$\sqrt{3}$x+t与坐标轴交于点B，C，连结AC，如果∠ACD=90°，则t=-$\frac{5\sqrt{3}}{3}$．