题目内容
3. 如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6$\sqrt{3}$米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).
如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为6$\sqrt{3}$米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°(结果精确到0.1).(1)求树AB与测角仪EF的水平距离DF的长;
(2)求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,$\sqrt{3}$≈1.73)
分析 (1)桶解直角三角形BCD来求CD的长度,则DF=CD+CF;
(2)由(1)求得DF的长,进而求得GF的长,然后在直角三角形BGE中即可求得BG的长,从而求得树高.
解答 解:(1)在Rt△BCD中:CD=BC•cos30°=$6\sqrt{3}×\frac{{\sqrt{3}}}{2}$=9,
∴DF=10;
(2)在Rt△AGE中,∵∠AEG=45°,
∴AG=EG=10,
在Rt△BGE中,BG=EG•tan20°=10×0.36=3.6.
∴AB=10-3.6=6.4
答:树AB的高为6.4米.
点评 本题考查了解直角三角形的应用,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
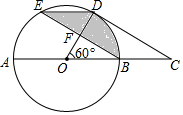 如图,在⊙O中,AB是直径,D、E为⊙O上两点,过点D作⊙O的切线CD交AB的延长线于点C,OD与BE交于F点,四边形BCDE是平行四边形.
如图,在⊙O中,AB是直径,D、E为⊙O上两点,过点D作⊙O的切线CD交AB的延长线于点C,OD与BE交于F点,四边形BCDE是平行四边形. 如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.
如图,点A的坐标为(-5,0),直线y=$\sqrt{3}$x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=-$\frac{5\sqrt{3}}{3}$.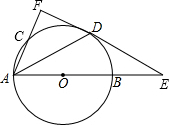 如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
如图,AB是⊙O的直径,且AB=6,C是⊙O上一点,D是$\widehat{BC}$的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.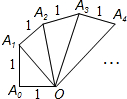 如图中的螺旋由一系列直角三角形组成,则第2017个三角形的面积为$\frac{\sqrt{2017}}{2}$.
如图中的螺旋由一系列直角三角形组成,则第2017个三角形的面积为$\frac{\sqrt{2017}}{2}$.