题目内容
1.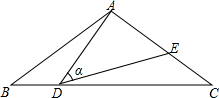 如图,在△ABC中,AB=AC=10,BC=16,D是边BC上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,给出下列结论:①图中有2对相似三角形;②线段CE长的最大值为6.4;③当AD=DC时,BD的长为$\frac{39}{4}$.其中正确的结论是( )
如图,在△ABC中,AB=AC=10,BC=16,D是边BC上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,给出下列结论:①图中有2对相似三角形;②线段CE长的最大值为6.4;③当AD=DC时,BD的长为$\frac{39}{4}$.其中正确的结论是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 ①根据有两组对应角相等的三角形相似即可证明;
②由△CDE∽△BAD,BC=16,AB=10,设BD=y,CE=x,可得$\frac{AB}{DC}$=$\frac{BD}{CE}$,即$\frac{10}{16-y}$=$\frac{y}{x}$,整理得:y2-16y+64=64-10x,即(y-8)2=64-10x,由64-10x≥0即可解决问题.
③当DA=DC时,易证△ADC∽△BAC,得$\frac{AD}{BA}$=$\frac{AC}{BC}$,由此即可解决问题.
解答 解:∵AB=AC,
∴∠B=∠C,
∵∠∠ADE=∠B=α,
∴∠ADE=∠C,∵∠DAE=∠DAC,
∴△DAE∽△CAD,
∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,
∴∠ECD=∠BAD,∵∠C=∠B,
∴△ABD∽△DCE,
∴图中有2对相似三角形,故①正确,
∵△CDE∽△BAD,BC=16,AB=10,
设BD=y,CE=x,
∴$\frac{AB}{DC}$=$\frac{BD}{CE}$,
∴$\frac{10}{16-y}$=$\frac{y}{x}$,
整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,
∵64-10x≥0
∴0<x≤6.4,
∴CE的最大值为6.4,故②正确,
当DA=DC时,易证△ADC∽△BAC,
∴$\frac{AD}{BA}$=$\frac{AC}{BC}$,
∴$\frac{AD}{10}$=$\frac{10}{16}$,
∴AD=$\frac{25}{4}$,
∴BD=16-$\frac{25}{4}$=$\frac{39}{4}$,故③正确.
故选D.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质、不等式的性质,二元二次方程等知识,解题的关键是熟练掌握相似三角形的判定和性质,学会用配方法确定变量x的取值范围,属于中考常考题型.

| x | … | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | … |
| A. | y1>y2 | B. | y1≤y2 | C. | y1<y2 | D. | y1≥y2 |
| A. | m<2 | B. | m>1 | C. | m>-2 | D. | m<-1 |
| A. | 5$\sqrt{a}$-3$\sqrt{a}$=2$\sqrt{a}$ | B. | $\sqrt{1\frac{9}{16}}$=1$\frac{3}{4}$ | C. | $\sqrt{2\frac{2}{3}}$=2$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{3}$+$\sqrt{2}$=$\frac{1}{\sqrt{3}-\sqrt{2}}$ |
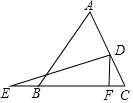 如图,在△ABC中,D在AC边上,DF⊥BC于F,∠E+∠A=∠C,AB=DE.若CF=$\sqrt{5}$,则BE=2$\sqrt{5}$.
如图,在△ABC中,D在AC边上,DF⊥BC于F,∠E+∠A=∠C,AB=DE.若CF=$\sqrt{5}$,则BE=2$\sqrt{5}$.