题目内容
8. 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
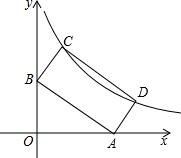
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.(1)求k的值;
(2)若矩形ABCD的顶点C,D在双曲线y=$\frac{k}{x}$(x>0)上,顶点A,B分别在x轴,y轴的正半轴上,且AB=2BC,求点C的坐标.
分析 (1)将点P的坐标代入双曲线解析式中解答即可;
(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,易证得△CFB∽△BOA,得到C($\frac{1}{2}$b,$\frac{1}{2}$a+b),解得a的值,即可求出点C的坐标.
解答 解:(1)∵点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上,
∴k=($\sqrt{5}$+1)($\sqrt{5}$-1)=4;
(2)过点D作DE⊥OA于点E,过点C作CF⊥OB于点F,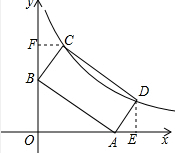
∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠CBA=∠BAD=90°,
∴∠FBC+∠OBA=90°,
∵∠CFB=∠BOA=90°,
∴∠FCB+∠FBC=90°,
∴∠FBC=∠OAB,
∴△CFB∽△ABO,
∴$\frac{CF}{OB}$=$\frac{BF}{OA}$=$\frac{BC}{AB}$=$\frac{1}{2}$,
∴CF=$\frac{1}{2}$OB,BF=$\frac{1}{2}$OA,
同理AE=$\frac{1}{2}$OB,DE=$\frac{1}{2}$OA,
设A(a,0),B(0,b),
∴OA=a,OB=b,
∴CF=AE=$\frac{1}{2}$b,BF=DE=$\frac{1}{2}$a
则D(a+$\frac{1}{2}$b,$\frac{1}{2}$a)C($\frac{1}{2}$b,$\frac{1}{2}$a+b),
∵点C,D在双曲线y=$\frac{k}{x}$(x>0)上,
∴(a+$\frac{1}{2}$b)•($\frac{1}{2}$a)=($\frac{1}{2}$b)•($\frac{1}{2}$a+b)=4,
∴a=b=$\frac{4\sqrt{3}}{3}$,
∴C($\frac{2\sqrt{3}}{3}$,2$\sqrt{3}$).
点评 此题考查了待定系数法求函数的解析式、矩形的性质与判定、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,综合性很强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
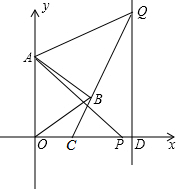 如图,已知等边△AOB的顶点O与原点重合,点A的坐标为(0,2$\sqrt{3}$),点P(t,0)为x轴上一动点(不与O重合).连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QB并延长交x轴于点C.过Q作x轴的垂线,垂足为D.
如图,已知等边△AOB的顶点O与原点重合,点A的坐标为(0,2$\sqrt{3}$),点P(t,0)为x轴上一动点(不与O重合).连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QB并延长交x轴于点C.过Q作x轴的垂线,垂足为D.