题目内容
13.先化简,再求值:(1)当a=$\frac{1}{10}$时,求$\frac{a+1}{{a}^{2}-1}$-$\frac{a+1}{1-a}$的值;
(2)设x=3y,求$\frac{4xy}{{x}^{2}-{y}^{2}}$-$\frac{x+y}{x-y}$的值.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x=3y代入进行计算即可.
解答 解:(1)原式=$\frac{1}{a-1}$+$\frac{a+1}{a-1}$
=$\frac{a+2}{a-1}$,
当a=$\frac{1}{10}$时,原式=$\frac{\frac{1}{10}+2}{\frac{1}{10}-1}$=-$\frac{21}{9}$;
(2)原式=$\frac{4xy}{(x+y)(x-y)}$-$\frac{(x+y)^{2}}{(x-y)(x+y)}$
=$\frac{4xy-(x+y)^{2}}{(x+y)(x-y)}$,
当x=3y时,原式=$\frac{4y•3y-{(3y+y)}^{2}}{(3y+y)(3y-y)}$=$\frac{12{y}^{2}-16{y}^{2}}{8{y}^{2}}$=$\frac{-4{y}^{2}}{8{y}^{2}}$=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3. 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求
对于两人的作法,下列判断何者正确?( )
 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:(甲)作AB的中垂线,交BC于P点,则P即为所求
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求
对于两人的作法,下列判断何者正确?( )
| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
1.如表给出A、B、C三种上宽带网的收费方式.
选取哪种方式能节省上网费?
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
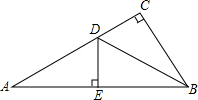 如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.
如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.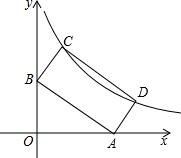 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上. 如图,直线AB,CD相交于点O,若∠BOD=$\frac{1}{2}$∠BOD+18°,则∠AOD=144°.
如图,直线AB,CD相交于点O,若∠BOD=$\frac{1}{2}$∠BOD+18°,则∠AOD=144°.