题目内容
16.解不等式:|x-1|+|x+1|≤3.分析 由于x的符号不能确定,故应分x<-1,-1≤x≤1或x>1三种情况进行讨论.
解答 解:当x<-1时,原不等式可化为1-x-(x+1)≤3,解得x≥-$\frac{3}{2}$,即-$\frac{3}{2}$≤x<-1;
当-1≤x≤1时,原不等式可化为1-x+x+1≤3,此时不等式无解;
当x>1时,原不等式可化为x-1+x+1≤3,解得x≤$\frac{3}{2}$,即1≤x<$\frac{3}{2}$.
故不等式组的解集为:-$\frac{3}{2}$≤x<-1或1≤x<$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式,在解答此题时要进行分类讨论.

练习册系列答案
相关题目
1.如表给出A、B、C三种上宽带网的收费方式.
选取哪种方式能节省上网费?
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
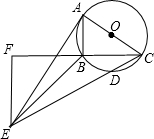 如图,△ABC是⊙O的内接三角形,AC经过点O,AB=3,BC=4,D是劣弧BC上一点,连接CD并延长到点E,使得5CD=CE,连接AE、BE,过点E作BC的垂线,交CB的延长线于点F.
如图,△ABC是⊙O的内接三角形,AC经过点O,AB=3,BC=4,D是劣弧BC上一点,连接CD并延长到点E,使得5CD=CE,连接AE、BE,过点E作BC的垂线,交CB的延长线于点F.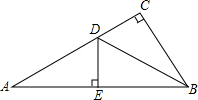 如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.
如图,在△ABC中,∠C=90°,AB的垂直平分线交AC于D,垂足为E,如果∠A=30°,DE=4cm,求∠DBC的度数和CD的长.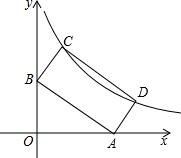 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.