题目内容
17. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的是②③(填编号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的是②③(填编号)
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:根据图象知道
当x=1时,y=a+b+c>0,故①错误;
当x=-1时,y=a-b+c<0,故②正确;
∵抛物线开口朝下,
∴a<0,
∵对称轴x=-$\frac{b}{2a}$(0<x<1),
∴2a<-b,
∴b+2a<0,故③正确;
∵对称轴x=-$\frac{b}{2a}$(0<x<1),
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故④错误.
故答案为:②③.
点评 此题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
8.一组数据4,6,6,a的中位数与平均数相同,则a的值为( )
| A. | 4 | B. | 8 | C. | 4或8 | D. | 4或7 |
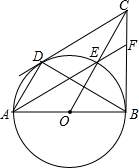 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )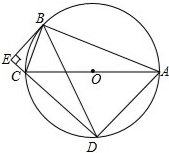 ⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.
⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.