Question

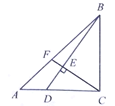
【题目】如图，在△ABC中，BA＝BC，以AB为直径作半圆⊙O，交AC于点D，过点D作DE⊥BC，垂足为点E．

（1）求证：DE为⊙O的切线；

（2）求证：BD2＝ABBE．

Answer 1

【答案】(1)证明见解析；（2）证明见解析.

【解析】

（1）连接OD、BD，根据圆周角定理可得∠ADB＝90°，继而得出点D是AC中点，判断出OD是三角形ABC的中位线，利用中位线的性质得出∠ODE＝90°，这样可判断出结论．

（2）根据题意可判断△BED∽△BDC，从而可得BD2＝BCBE，将BC替换成AB即可得出结论．

证明：（1）连接OD、BD，则∠ADB＝90°（圆周角定理），

∵BA＝BC，

∴CD＝AD（三线合一），

又∵AO＝OB，

∴OD是△ABC的中位线，

∴OD∥BC，

∵∠DEB＝90°，

∴∠ODE＝90°，即OD⊥DE，

故可得DE为⊙O的切线；

（2）∵∠EBD＝∠DBC，∠DEB＝∠CDB，

∴△BED∽△BDC，

∴，

又∵AB＝BC，

∴ ，

故BD2＝ABBE．