题目内容
20. 如图,四边形ABCD是菱形,点E,点F分别是CD,AD上的点,CE=DF,DE=2CE,AE,CF交于点O,则AO:OE=6.
如图,四边形ABCD是菱形,点E,点F分别是CD,AD上的点,CE=DF,DE=2CE,AE,CF交于点O,则AO:OE=6.
分析 根据题意得出过点F作FN∥DC交AE于点N,得出△AFN∽△ADB,进而表示出EC,EO,AO的长,即可得出答案.
解答 解:过点F作FN∥DC交AE于点N,
∵FN∥DC,
∴△AFN∽△ADB,
∴$\frac{AF}{AD}$=$\frac{FN}{DE}$,
∵CE=DF,DE=2CE,四边形ABCD是菱形,
∴AF=DE,AF=2DF,
∴$\frac{2}{3}$=$\frac{FN}{DE}$,
设EC=x,则DE=2x,AF=2x,DF=x,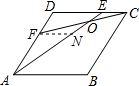
故$\frac{2}{3}$=$\frac{FN}{DE}$=$\frac{FN}{2x}$,
解得:FN=$\frac{4x}{3}$,
∴$\frac{FN}{EC}$=$\frac{\frac{4x}{3}}{x}$=$\frac{4}{3}$,
∵FN∥EC,
∴△FNO∽△CEO,
∴$\frac{FN}{EC}$=$\frac{NO}{EC}$=$\frac{4}{3}$,
设NO=4a,则EO=3a,
∵$\frac{AN}{NE}$=$\frac{2}{1}$=$\frac{AN}{7a}$,
∴AN=14a,
故AO=14a+4a=18a,
∴$\frac{AO}{EO}$=$\frac{18a}{3a}$=6.
故答案为:6.
点评 此题主要考查了相似三角形的判定与性质,正确作出辅助线是解题关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
9.已知⊙O的面积为3π,则其内接正三角形的面积为( )
| A. | 9$\sqrt{3}$ | B. | $\frac{9\sqrt{3}}{4}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{9\sqrt{6}}{4}$ |
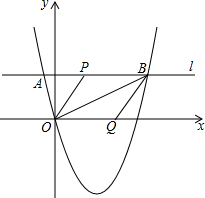 如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$.
如图,抛物线y=ax2+3(a-1)x(a>0)经过点A(-3,m),过点A作直线l平行于x轴与抛物线交于另一点B,在x轴上取点Q,连接BQ,使得∠QBO=∠ABO,过点O作OP平行BQ交l于点P,若AP=$\frac{1}{2}$AB,则a的值为$\frac{1}{9}$. 在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.
在某次学校安全知识抢答赛中,九年级参赛的10名学生的成绩统计图如图所示.这10名学生的参赛成绩的中位数是90分.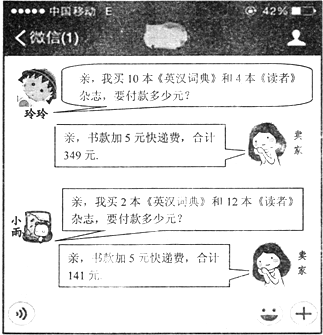
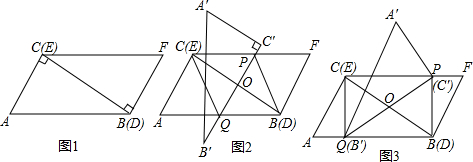
 如图,下列能判定AB∥CD的条件有( )个
如图,下列能判定AB∥CD的条件有( )个