题目内容
 如图,Rt△ABC中,∠C=90°,BC=
如图,Rt△ABC中,∠C=90°,BC=| 3 |
考点:扇形面积的计算
专题:
分析:先连接BE,BO,EO,由勾股定理得出AB的长,求出∠BAC=30°,∠BOE=2∠BAC=60°,因为S△ABC=
×BC×AC=
×3×
=
,△BOE和△ABE同底等高,△BOE和△ABE面积相等,用S△ABC-S扇形BOE即得阴影部分面积.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
解答:解:连接BE,BO,EO,

∵∠C=90°,BC=
,AC=3,
∴AB=
=2
,
∴∠BAC=30°.
∴∠BOE=2∠BAC=60°.
∴S△ABC=
×BC×AC=
×3×
=
.
∵△BOE和ABE同底等高,
∴△BOE和△ABE面积相等,
∴阴影部分的面积为:S△ABC-S扇形BOE=
-
=
-
.
故答案为:
-
.

∵∠C=90°,BC=
| 3 |
∴AB=
| BC2+AC2 |
| 3 |
∴∠BAC=30°.
∴∠BOE=2∠BAC=60°.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
∵△BOE和ABE同底等高,
∴△BOE和△ABE面积相等,
∴阴影部分的面积为:S△ABC-S扇形BOE=
| 3 |
| 2 |
| 3 |
| 60π×22 |
| 360 |
3
| ||
| 2 |
| 2π |
| 3 |
故答案为:
3
| ||
| 2 |
| 2π |
| 3 |
点评:此题主要考查了扇形的面积计算以及三角形面积求法等知识,根据已知得出△BOE和△ABE面积相等是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知AB∥CD,∠1=110°,则∠A的度数是( )
如图,已知AB∥CD,∠1=110°,则∠A的度数是( )| A、70° | B、100° |
| C、110° | D、130° |
2014年一季度,全国新增就业人数为416万人,用科学记数法表示416万正确的是( )人.
| A、4.16×107 |
| B、4.16×106 |
| C、4.16×105 |
| D、4.16×104 |
 如图,将一张长方形纸片沿EF折叠后,点A、B分别落在点A′、B′的位置,A′B′交BC于点G.若∠AEF=n°,则∠FGB′=
如图,将一张长方形纸片沿EF折叠后,点A、B分别落在点A′、B′的位置,A′B′交BC于点G.若∠AEF=n°,则∠FGB′=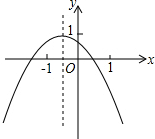 如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为正确的有
如图所示的二次函数图象,以下四个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为正确的有 某公司为适应市场竞争,开发研制了一种新产品A,并制定了生产、销售计划.开始的10天,只生产不销售,随后的40天,边生产边销售(每天的生产量、销售量是一定的),库存量y(吨)与时间x(天)的关系如图所示,根据图象回答下列问题:
某公司为适应市场竞争,开发研制了一种新产品A,并制定了生产、销售计划.开始的10天,只生产不销售,随后的40天,边生产边销售(每天的生产量、销售量是一定的),库存量y(吨)与时间x(天)的关系如图所示,根据图象回答下列问题: