题目内容
17.开学初,某中学在重百商场购进甲、乙两种品牌的足球,购买甲品牌足球花费了2400元,购买乙品牌足球花费了1600元,且购买甲品牌足球数量是购买乙品牌足球数量的2倍,已知购买一个乙品牌足球比购买一个甲品牌足球多花20元.(1)求购买一个甲品牌、一个乙品牌的足球各需多少元?
(2)为响应“足球进校园”的号召,学校决定再次购进甲,乙两种品牌足球共50个,恰逢重百商场对两种品牌足球的售价进行调整,其中甲品牌足球售价比第一次购买时提高了5%,乙品牌足球按第一次购买时售价的9折出售,若这所中学此次购买甲,乙两种品牌足球的总费用不超过3360元,则此次最多可购买多少个乙品牌足球?
分析 (1)设购买一个甲品牌的足球需x元,则购买一个乙品牌的足球需(x+20)元,根据购买甲种足球数量是购买乙种足球数量的2倍列出方程解答即可;
(2)设这所学校再次购买y个乙品牌的足球,根据题意列出不等式解答即可.
解答 解:(1)设购买一个甲品牌的足球需x元,则购买一个乙品牌的足球需(x+20)元,
由题意可得:$\frac{2400}{x}$=$\frac{1600}{x+20}$×2,
解得:x=60,
经检验x=60是原方程的解,
答:购买一个甲品牌的足球需60元,则购买一个乙品牌的足球需80元;
(2)设这所学校再次购买y个乙种足球,
由题意可得:60×(1+5%)×(50-y)+80×0.9y≤3360,
解得:y≤23$\frac{1}{3}$,
由题意可得,最多可购买23个乙品牌的足球,
答:此次最多可购买23个乙品牌足球.
点评 本题考查分式方程、一元一次不等式的应用,关键是根据数量作为等量关系列出方程,根据总费用作为不等关系列出不等式求解.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.比-1小2015的数是( )
| A. | -2014 | B. | 2016 | C. | -2016 | D. | 2014 |
5.在平面直角坐标系中,点A(3,-5)所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.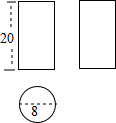 如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )| A. | 128πcm2 | B. | 160πcm2 | C. | 176πcm2 | D. | 192πcm2 |
9.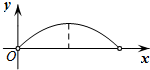 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界逆时针运动一周,设点P走过的路程为x,线段MP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界逆时针运动一周,设点P走过的路程为x,线段MP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
 已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界逆时针运动一周,设点P走过的路程为x,线段MP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )
已知点M为某封闭图形边界上一定点,动点P从点M出发,沿其边界逆时针运动一周,设点P走过的路程为x,线段MP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )| A. | 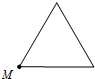 | B. | 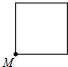 | C. |  | D. | 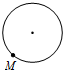 |
7.将18个大小重量完全一样的彩球放入一个袋中,其中6个是白色的,5个是黄色的,4个是绿色的,3个是红色的,任意摸出一个彩球是红色的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
 如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )
如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )



 如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).
如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).