题目内容
11. 如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )
如图,在菱形ABCD中,点O在对角线AC上,且AO=2CO,连接OB、OD,若OB=OC=OD,AC=3,则菱形的边长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由AO=2CO,OB=OC=OD,AC=3,可求得OC的长,然后由菱形的对角线平分对角以及等腰三角形的性质,证得∠CAB=∠CBO,继而证得△BCO∽△ACB,然后由相似三角形的对应边成比例,求得答案.
解答 解:∵AO=2CO,OB=OC=OD,AC=3,
∴OA=2,OB=OC=OD=1,
∴∠ACB=∠CBO,
∵四边形ABCD是菱形,
∴∠DAC=∠BAC=∠ACB,
∴∠CBO=∠CAB,
∵∠BCO=∠ACB,
∴△BCO∽△ACB,
∴BC:AC=OC:BC,
∴BC2=AC•OC=3,
∴BC=$\sqrt{3}$.
故选A.
点评 此题考查了菱形的性质、等腰三角形的性质以及相似三角形的判定与性质.注意证得△BCO∽△ACB是解此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.在下列性质中,矩形具有而菱形不一定有的是( )
| A. | 四个角是直角 | B. | 四条边相等 | C. | 对角线互相垂直 | D. | 对角线互相平分 |
3.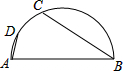 如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
 如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )
如图,AB是半圆的直径,D是弧AC的中点,∠ABC=50°,则∠DAB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
20.3-2可以表示为( )
| A. | $\frac{1}{3×3}$ | B. | -$\frac{1}{3×3}$ | C. | 3×3 | D. | 3+3 |
1.下列各数中,绝对值最大的数是( )
| A. | 1 | B. | 0 | C. | -3 | D. | -2 |
 如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )
如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )



 如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).
如图,直线y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx-2经过A,B,C,点B坐标为(-1,0).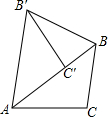 如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为69°.
如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为69°.