题目内容
 如图,∠BCA=90°,CD⊥AB,E为AB的中点,∠DCA:∠BCD=3:1,∠DCE的度数为
如图,∠BCA=90°,CD⊥AB,E为AB的中点,∠DCA:∠BCD=3:1,∠DCE的度数为考点:直角三角形斜边上的中线
专题:
分析:根据比例求出∠BCD,根据直角三角形两锐角互余求出∠B,再根据直角三角形斜边上的中线等于斜边的一半可得BE=CE,利用等边对等角可得∠B=∠BCE,然后根据∠DCE=∠BCE-∠BCD代入数据计算即可得解.
解答:解:∵∠DCA:∠BCD=3:1,∠BCA=90°,
∴∠BCD=90×
=22.5°,
∵CD⊥AB,
∴∠B=90°-22.5°=67.5°,
∵E为AB的中点,
∴BE=CE,
∴∠B=∠BCE=67.5°,
∴∠DCE=∠BCE-∠BCD,
=67.5°-22.5°,
=45°.
故答案为:45°.
∴∠BCD=90×
| 1 |
| 1+3 |
∵CD⊥AB,
∴∠B=90°-22.5°=67.5°,
∵E为AB的中点,
∴BE=CE,
∴∠B=∠BCE=67.5°,
∴∠DCE=∠BCE-∠BCD,
=67.5°-22.5°,
=45°.
故答案为:45°.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半,直角三角形两锐角互余的性质,等边对等角的性质,熟记各性质是解题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
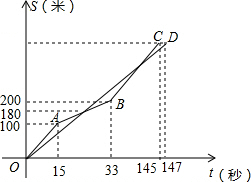 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
 如图的直角△ABC中,∠BAC=90°,AF⊥BC于点F,BD平分∠ABC交AF于点E,交AC于点D,试判定△ADE的形状并说明理由.
如图的直角△ABC中,∠BAC=90°,AF⊥BC于点F,BD平分∠ABC交AF于点E,交AC于点D,试判定△ADE的形状并说明理由. 如图,量角器外缘边上A、P、Q三点,它们所表示的读数分别是180°,76°,26°,则∠PAQ的大小为
如图,量角器外缘边上A、P、Q三点,它们所表示的读数分别是180°,76°,26°,则∠PAQ的大小为 ,它的实际号是
,它的实际号是