题目内容
12. 如图,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3下面四个结论:①AO:AC=1:3;②△ADO∽△CBO;③S△ADO:S△CBO=1:9;④若△CBO的周长为m,则△ADO的周长为3m,其中正确的是( )
如图,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3下面四个结论:①AO:AC=1:3;②△ADO∽△CBO;③S△ADO:S△CBO=1:9;④若△CBO的周长为m,则△ADO的周长为3m,其中正确的是( )| A. | ①②③④ | B. | ②③④ | C. | ②③ | D. | ③④ |
分析 由AD∥BC,推出△ADO∽△BCO,根据相似三角形的性质得到AO:OC=AD:BC=$\frac{1}{3}$,S△ADO:S△CBO=($\frac{AD}{BC}$)2=1:9,△CBO的周长:△ADO的周长=$\frac{BC}{AD}$=3,于是得到结论.
解答 解:∵AD∥BC,
∴△ADO∽△BCO,故②正确;
∴AO:OC=AD:BC=$\frac{1}{3}$,S△ADO:S△CBO=($\frac{AD}{BC}$)2=1:9,故③正确;
∴AO:AC=1:4,故①错误;
∵△ADO∽△BCO,
∴△CBO的周长:△ADO的周长=$\frac{BC}{AD}$=3,
∵△CBO的周长为m,则△ADO的周长为$\frac{1}{3}$m;故④错误;
故选C.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
 某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )
某种零件模型如图所示,该几何体(空心圆柱)的主视图是( )| A. |  | B. |  | C. |  | D. |  |
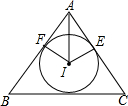 如图所示,在△ABC中,AB=AC=10.BC=12,△ABC的内切圆⊙I与AB、AC切于F、E,试求⊙I的半径.
如图所示,在△ABC中,AB=AC=10.BC=12,△ABC的内切圆⊙I与AB、AC切于F、E,试求⊙I的半径. 如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°.
如图,在圆内接四边形ABCD中,若∠A=60°,则∠C的大小为120°.