题目内容
5.多项式$\frac{1}{2}$x|m|y-(m-3)xy+7是关于x、y的四次三项式,则m的值是( )| A. | 3或-3 | B. | -3 | C. | 4或-4 | D. | 3 |
分析 根据四次三项式的定义可知,该多项式的最高次数为4,项数是3,所以可确定m的值.
解答 解:∵多项式$\frac{1}{2}$x|m|y-(m-3)x+7是关于x的四次三项式,
∴|m|=3,-(m-3)≠0,
∴m=-3.
故选:B.
点评 本题考查了与多项式有关的概念,解题的关键是理解四次三项式的概念,多项式中每个单项式叫做多项式的项,有几项叫几项式,这些单项式中的最高次数,就是这个多项式的次数.

练习册系列答案
相关题目
20.一列数a1,a2,a3,…an,其中a1=-1,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$,则a2014=( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 2014 |
15.已知5x2y3-3xmy+6是关于x,y的六次多项式,则m的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
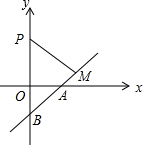 如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$. 如图,已知在等腰△ABC中,∠A=∠B=30°过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°过点C作CD⊥AC交AB于点D.