题目内容
1.抛物线y=x2-2x+m与x轴只有一个交点,则m的值为1.分析 由抛物线y=x2-2x+m与x轴只有一个交点可知,对应的一元二次方程x2-2x+m=0,根的判别式△=b2-4ac=0,由此即可得到关于m的方程,解方程即可求得m的值.
解答 解:∵抛物线y=x2-2x+m与x轴只有一个交点,
∴△=0,
∴b2-4ac=22-4×1×m=0;
∴m=1.
故答案为:1.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可转化为解关于x的一元二次方程.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.

练习册系列答案
相关题目
11.学校校运动会期间,小华花100元从批发部批发了矿泉水和可乐共74瓶,到学校卖,矿泉水和可乐的批发价和零售价如表所示:
求他运动会期间卖完这些矿泉水和可乐可以赚多少元?
| 饮料 | 矿泉水 | 可乐 |
| 批发价(元/瓶) | 0.8 | 2.5 |
| 零售价(元/瓶) | 1 | 3 |
12.下列等式中,从等号左边到右边的变形是因式分解的是( )
| A. | x2-9+8x=(x-3)(x+3)+8x | B. | -5x2y3=-5xy•(xy2) | ||
| C. | x2-4x-5=x(x-4-$\frac{5}{x}$) | D. | -x2+2xy=-x(x-2y) |
10.上网费包括网络使用费(每月38元)和上网通讯费(每小时2元),某电信局对拨号上网用户实行优惠,具体优惠政策如下:
(1)若小明家四月份上网28小时,应缴上网费多少?
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
| 上网时间 | 优惠标准 |
| 0~30小时(不超过30) | 无优惠 |
| 30~50小时(不超过50) | 通讯费优惠30% |
| 50~100小时(不超过100) | 通讯费优惠40% |
| 100小时以上 | 通讯费优惠50% |
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
11.有下列四个命题,其中正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 三点确定一个圆 | |
| C. | 三角形的内心到三角形三个顶点的距离相等 | |
| D. | 相等的弧所对的圆心角相等 |
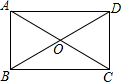 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$.
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠COD=60°,则AD的长为3$\sqrt{3}$.