题目内容
10．已知$\sqrt{（x-2）^{2}}$+|x-3|=1，则x的取值范围是2≤x≤3．分析 利用绝对值以及二次根式的性质得出x-2≥0，x-3≤0，进而求出x的取值范围．
解答 解：∵$\sqrt{（x-2）^{2}}$+|x-3|=1，
∴$\sqrt{（x-2）^{2}}$=x-2，|x-3|=3-x，
∴x-2≥0，x-3≤0，
解得：2≤x≤3．
故答案为：2≤x≤3．
点评 此题主要考查了二次根式的性质与绝对值，得出关于x的不等关系是解题关键．
练习册系列答案
寒假学与练系列答案
相关题目
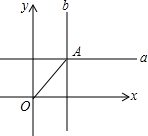如图，在平面直角坐标系xOy中，分别平行x、y轴的两直线a、b相交于点A（3，4）．连接OA，