题目内容
15. 如图,在?ABCD中,E是AD上一点,且EM∥AD,EN∥CD,则下列式子中错误的是( )
如图,在?ABCD中,E是AD上一点,且EM∥AD,EN∥CD,则下列式子中错误的是( )| A. | $\frac{AM}{BM}=\frac{DE}{BE}$ | B. | $\frac{AM}{AB}=\frac{CN}{CB}$ | C. | $\frac{ME}{BC}=\frac{NE}{AB}$ | D. | $\frac{BE}{BD}=\frac{NE}{CB}$ |
分析 由EM∥AD,EN∥CD,根据平行线分线段成比例定理,可得证得$\frac{AM}{MB}=\frac{DE}{BE}$,$\frac{AM}{AB}$=$\frac{DE}{DB}$=$\frac{CN}{CB}$,$\frac{ME}{AD}=\frac{BE}{BD}$,$\frac{EN}{CD}=\frac{BE}{BD}$,又由四边形ABCD是平行四边形,易得$\frac{ME}{BC}=\frac{NE}{AB}$,则可求得答案.
解答 解:A、∵EM∥AD,
∴$\frac{AM}{MB}=\frac{DE}{BE}$,故正确;
B、∵EM∥AD,EN∥CD,
∴$\frac{AM}{AB}$=$\frac{DE}{DB}$,$\frac{DE}{DB}$=$\frac{CN}{CB}$,
∴$\frac{AM}{AB}$=$\frac{CN}{CB}$,故正确;
C、∵EM∥AD,EN∥CD,
∴$\frac{ME}{AD}=\frac{BE}{BD}$,$\frac{EN}{CD}=\frac{BE}{BD}$,
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,
∴$\frac{ME}{BC}=\frac{NE}{AB}$,故正确;
D、∵EN∥CD,
∴$\frac{EN}{CD}=\frac{BE}{BD}$,故错误.
故选D.
点评 此题考查了平行线分线段成比例定理.注意掌握线段的对应关系.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.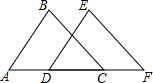 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
 如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )
如图,已知点A D C F在同一直线上,AB=DE,AD=CF,添加下列条件后,仍不能判断△ABC≌△DEF的是( )| A. | BC=EF | B. | ∠A=∠EDF | C. | AB∥DE | D. | ∠BCA=∠F |
20.若|x+1|+(y-2)2=0,则xy的值是( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
5.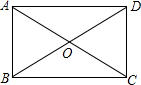 如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
 如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )
如图,在矩形ABCD中,AB=2,∠AOB=60°,则OB的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
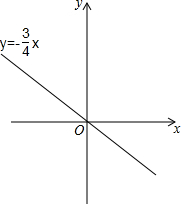 一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C.
一次函数y=-$\frac{3}{4}$x的图象如图所示,它与二次函数y=ax2+4ax+c的图象交于A、B两点(其中点A在点B的右侧),与这个二次函数图象的对称轴交于点C. 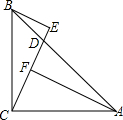 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,BE⊥CD,垂足为点E,AF⊥CD,垂足为点F,若$\frac{BD}{AD}$=$\frac{1}{2}$,AC=6$\sqrt{5}$,则DE=2. 如图,某广场为矩形ABCD,现准备在广场的内部修建照明灯,要求照明灯0到广场的两个人口A,D的距离相等,且到AB,BC两边的距离相等.
如图,某广场为矩形ABCD,现准备在广场的内部修建照明灯,要求照明灯0到广场的两个人口A,D的距离相等,且到AB,BC两边的距离相等. 如图,是y关于x的函数的图象,则不等式kx+b≤0的解集在数轴上可表示为( )
如图,是y关于x的函数的图象,则不等式kx+b≤0的解集在数轴上可表示为( )


