题目内容
7.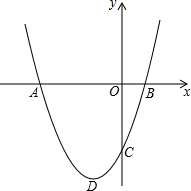 已知二次函数y=x2+2x-3的图象与x轴、y轴交于A、B、C三点,顶点为D.
已知二次函数y=x2+2x-3的图象与x轴、y轴交于A、B、C三点,顶点为D.(1)求A、B、C、D的坐标;
(2)根据图象回答:
当x为何值时,x2+2x-3=0,
当x为何值时,x2+2x-3<0,
当x为何值时,x2+2x-3>0.
分析 (1)先令y=0求出x的值,再令x=0求出y的值即可得出A、B、C的坐标,把二次函数化为顶点式的形式即可得出D点坐标;
(2)根据(1)中A、B两点的坐标即可得出不等式的解集.
解答 解:(1)∵令y=0,则x=1或-3;令x=0,则y=-3,
∴A(-3,0),B(1,0),C(0,-3);
∵二次函数的解析式可化为y=(x+1)2-4,
∴D(-1,-4);
(2)∵由(1)知,A(-3,0),B(1,0),
∴当x=-3或x=1时,x2+2x-3=0;
当-3<x<1时,x2+2x-3<0;
当x<-3或x>1时,x2+2x-3>0.
点评 本题考查的是二次函数与不等式组,根据题意利用数形结合求解是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
15.下列函数中,y是x的反比例函数的是( )
| A. | x(y-1)=1 | B. | y=$\frac{1}{x+1}$ | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=$\frac{3}{x}$ |
19.在下面四个图形中,能用三种方法表示同一个角的图形是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,点P是反比例函数y=$\frac{2}{x}$的图象上任一点,PA垂直于x轴,垂足为A,设△OAP的面积为S,则S的值为1.
如图,点P是反比例函数y=$\frac{2}{x}$的图象上任一点,PA垂直于x轴,垂足为A,设△OAP的面积为S,则S的值为1.
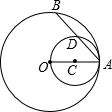 如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.
如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点D,求证:D是AB的中点.