题目内容
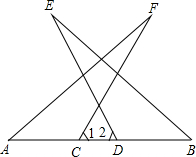 如图,已知∠A=∠B,∠1=∠2,AD=BC,求证:CF=DE.
如图,已知∠A=∠B,∠1=∠2,AD=BC,求证:CF=DE.考点:全等三角形的判定与性质
专题:证明题
分析:根据等式的性质就可以求出AC=BD,由邻补角的性质就可以得出∠ACF=∠BDE,从而得出△ACF≌△BDE,就可以得出结论.
解答:证明:∵∠1+∠ACF=180°,∠2+∠BDE=180°,且∠1=∠2,
∴∠ACF=∠BDE.
∵AD=BC,
∴AD-CD=BC-CD,
∴AC=BD.
在△ACF和△BDE中
,
∴△ACF≌△BDE(ASA),
∴CF=DE.
∴∠ACF=∠BDE.
∵AD=BC,
∴AD-CD=BC-CD,
∴AC=BD.
在△ACF和△BDE中
|
∴△ACF≌△BDE(ASA),
∴CF=DE.
点评:本题考查了邻补角的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
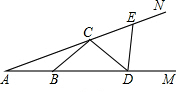 如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.
如图,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数.