题目内容
17.(1)解不等式2(x-1)≥x-5,并把解集表示在数轴上.(2)解不等式组$\left\{\begin{array}{l}3x+1>4\\ 4-2x≥0\end{array}\right.$.
分析 (1)先去括号,然后移项,合并同类项,即可求得;
(2)分别求出两个不等式的解集,求其公共解.
解答 解:(1)2(x-1)≥x-5,
2x-2≥x-5,
2x-x≥2-5,
x≥-3;
(2)$\left\{\begin{array}{l}{3x-1>4①}\\{4-2x≥0②}\end{array}\right.$
由①得,x>$\frac{5}{3}$,
由②得,x≤2,
所以,不等式的解集为$\frac{5}{3}$<x≤2.
点评 本题考查了解不等式(组),求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
5.若关于x的方程$\frac{x-1}{x-2}-\frac{m}{2-x}$=m无解,则m的值为( )
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 1或-1 |
9. 如图所示,此图的俯视图为( )
如图所示,此图的俯视图为( )
 如图所示,此图的俯视图为( )
如图所示,此图的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
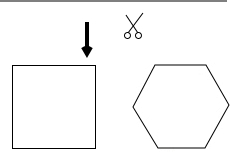 如图,用一根40cm长的铁丝剪成两段,分别做成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是$\frac{1}{3}$.
如图,用一根40cm长的铁丝剪成两段,分别做成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是$\frac{1}{3}$.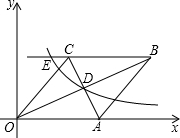 如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).
如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).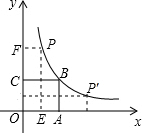 如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.
如图,正方形OABC的面积为16,点O为坐标原点,点B在双曲线y=$\frac{k}{x}$(x>0)上,点P(m,n)是双曲线上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,并设矩形OEPF在正方形OABC之外部分的面积为S.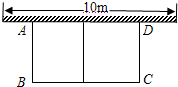 如图,一面利用墙,用总长度为24m的篱笆围成矩形花圃ABCD,其中中间用一段篱笆隔成两个小矩形,墙可利用的最大长度为10m,设AB的长为xm,矩形花圃ABCD的面积为ym2.
如图,一面利用墙,用总长度为24m的篱笆围成矩形花圃ABCD,其中中间用一段篱笆隔成两个小矩形,墙可利用的最大长度为10m,设AB的长为xm,矩形花圃ABCD的面积为ym2.