题目内容
2.关于x的方程x4+(2+k)x2+(3-k)x+3k=0有实数根且所有实数根的积为-6,求k的值及方程的解.分析 利用双十字相乘法把x4+(2+k)x2+(3-k)x+3k分解因式,再进一步利用根与系数的关系,分别探讨得出答案即可.
解答 解:分解因式:双十字相乘法:
x2 -x 3
x2+x K
∴(x2-x+3)(x2+x+K)=0,
∵x2-x+3=0或x2+x+K=0,
而x2-x+3=0无解,
∴x2+x+k=0,
∴x1+x2=-1,x1•x2=K,
∵所有实数根之积为-6,
∴K=-6,
∴x2+x-6=0,
x1=-3,x2=2.
点评 此题考查根与系数的关系,把原方程利用双十字相乘法因式分解是解决问题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
 图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.
图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.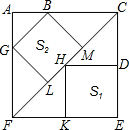 如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2
如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2